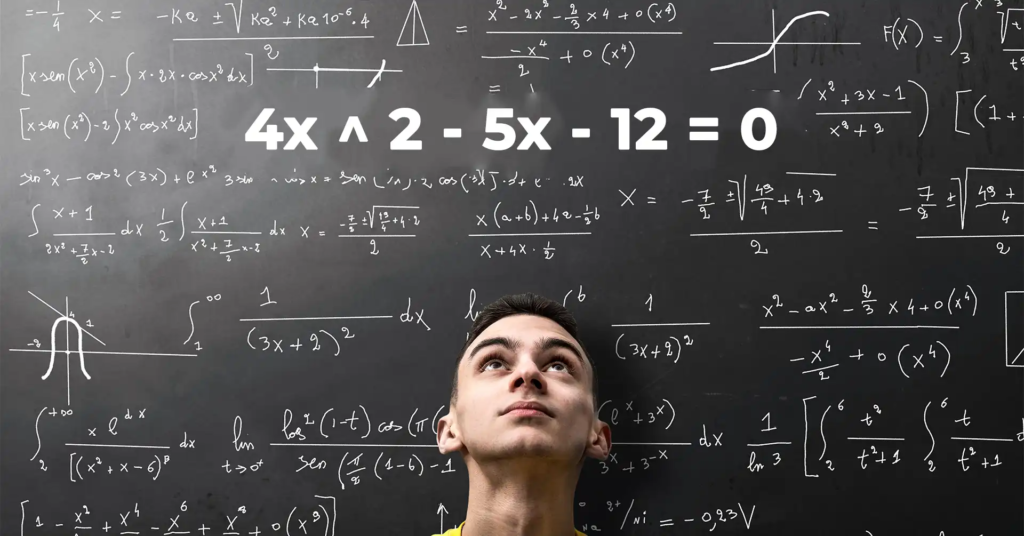When faced with the quadratic equation 4x ^ 2 – 5x – 12 = 0, many students and math enthusiasts might find themselves at a crossroads, wondering how to solve it effectively. This article delves into expert techniques for mastering this quadratic equation, providing a comprehensive guide that covers fundamental concepts, step-by-step solutions, and advanced insights. By the end of this piece, you’ll have a solid understanding of how to tackle similar equations confidently.
Understanding Quadratic Equations
Quadratic equations are a cornerstone of algebra, appearing frequently in various mathematical contexts and real-world applications. A quadratic equation is a second-degree polynomial equation in a single variable x, with the general form:
ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0
In our specific equation, 4x ^ 2 – 5x – 12 = 0, the coefficients are:
- a=4a = 4a=4
- b=−5b = -5b=−5
- c=−12c = -12c=−12
The solutions to this equation, also known as the roots, are the values of x that make the equation true.
Methods to Solve Quadratic Equations
- Factoring
Factoring is one of the simplest methods to solve a quadratic equation, but it requires the equation to be factorable into two binomials. To factor 4x ^ 2 – 5x – 12 = 0, we look for two numbers that multiply to a⋅c=4⋅−12=−48a \cdot c = 4 \cdot -12 = -48a⋅c=4⋅−12=−48 and add to b=−5b = -5b=−5.
After some consideration, we find that these numbers are 3 and -16. Rewriting the middle term using these numbers, we get:

4×2+3x−16x−12=04x^2 + 3x – 16x – 12 = 04×2+3x−16x−12=0
Next, we factor by grouping:
(4×2+3x)+(−16x−12)=0(4x^2 + 3x) + (-16x – 12) = 0(4×2+3x)+(−16x−12)=0
x(4x+3)−4(4x+3)=0x(4x + 3) – 4(4x + 3) = 0x(4x+3)−4(4x+3)=0
(x−4)(4x+3)=0(x – 4)(4x + 3) = 0(x−4)(4x+3)=0
Setting each factor to zero gives the solutions:
x−4=0or4x+3=0x – 4 = 0 \quad \text{or} \quad 4x + 3 = 0x−4=0or4x+3=0
x=4orx=−34x = 4 \quad \text{or} \quad x = -\frac{3}{4}x=4orx=−43
- Quadratic Formula
The quadratic formula is a universal method that can solve any quadratic equation. The formula is:
x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}x=2a−b±b2−4ac
Applying this to 4x ^ 2 – 5x – 12 = 0, we first compute the discriminant:
Δ=b2−4ac=(−5)2−4(4)(−12)=25+192=217\Delta = b^2 – 4ac = (-5)^2 – 4(4)(-12) = 25 + 192 = 217Δ=b2−4ac=(−5)2−4(4)(−12)=25+192=217
Then, we apply the quadratic formula:
x=−(−5)±2172(4)x = \frac{-(-5) \pm \sqrt{217}}{2(4)}x=2(4)−(−5)±217
x=5±2178x = \frac{5 \pm \sqrt{217}}{8}x=85±217
This yields two solutions:
x=5+2178andx=5−2178x = \frac{5 + \sqrt{217}}{8} \quad \text{and} \quad x = \frac{5 – \sqrt{217}}{8}x=85+217andx=85−217
- Completing the Square
Completing the square is another useful method, especially for deriving the quadratic formula. To complete the square for 4x ^ 2 – 5x – 12 = 0, follow these steps:
First, rewrite the equation:
4×2−5x=124x^2 – 5x = 124×2−5x=12
Divide all terms by 4:
x2−54x=3x^2 – \frac{5}{4}x = 3×2−45x=3
Next, add and subtract (−5/42)2\left(\frac{-5/4}{2}\right)^2(2−5/4)2:
x2−54x+(58)2=3+(58)2x^2 – \frac{5}{4}x + \left(\frac{5}{8}\right)^2 = 3 + \left(\frac{5}{8}\right)^2×2−45x+(85)2=3+(85)2
x2−54x+2564=3+2564x^2 – \frac{5}{4}x + \frac{25}{64} = 3 + \frac{25}{64}x2−45x+6425=3+6425
(x−58)2=21764\left(x – \frac{5}{8}\right)^2 = \frac{217}{64}(x−85)2=64217
Take the square root of both sides:
x−58=±21764x – \frac{5}{8} = \pm \sqrt{\frac{217}{64}}x−85=±64217
x−58=±2178x – \frac{5}{8} = \pm \frac{\sqrt{217}}{8}x−85=±8217
Solve for x:
x=58±2178x = \frac{5}{8} \pm \frac{\sqrt{217}}{8}x=85±8217
x=5+2178andx=5−2178x = \frac{5 + \sqrt{217}}{8} \quad \text{and} \quad x = \frac{5 – \sqrt{217}}{8}x=85+217andx=85−217
The Importance of Discriminant
The discriminant, Δ=b2−4ac\Delta = b^2 – 4acΔ=b2−4ac, is crucial in understanding the nature of the roots of a quadratic equation. If Δ>0\Delta > 0Δ>0, the equation has two distinct real roots. If Δ=0\Delta = 0Δ=0, it has one real root (a repeated root). The equation has two complex roots if Δ<0\Delta < 0Δ<0.
In our equation, the discriminant is 217, which is positive, indicating two distinct real roots.
Graphical Interpretation
Visualizing the quadratic equation on a graph can provide additional insights. The graph of 4×2−5x−12=04x ^ 2 – 5x – 12 = 04×2−5x−12=0 is a parabola. The roots are the x-intercepts of the parabola. The vertex form of a quadratic equation is helpful for graphing:
y=a(x−h)2+ky = a(x – h)^2 + ky=a(x−h)2+k
Where (h, k) is the vertex of the parabola. Completing the square helps to convert the standard form into vertex form.
Applications of Quadratic Equations
Quadratic equations are not just academic exercises; they have practical applications in various fields. For example:
- Physics: Describing the motion of objects under uniform acceleration.
- Engineering: Analyzing the stresses and strains in materials.
- Economics: Modeling profit and cost functions.
Practice Problems
Practice is essential to master solving quadratic equations. Here are a few additional problems for practice:
- 2×2−3x+1=02x^2 – 3x + 1 = 02×2−3x+1=0
- x2+6x+9=0x^2 + 6x + 9 = 0x2+6x+9=0
- 5×2−4x−1=05x^2 – 4x – 1 = 05×2−4x−1=0
Conclusion
Solving the quadratic equation 4x ^ 2 – 5x – 12 = 0 can be approached using several methods, each with advantages. Whether you choose factoring, the quadratic formula, or completing the square, understanding these techniques enhances your problem-solving skills in algebra. By practising and applying these methods, you can master quadratic equations and tackle even more complex mathematical challenges with ease.
Remember, the key to success in mathematics is practice and perseverance. With the expert techniques discussed in this article, you’re well on your way to quadratic mastery.
Do Read: Exploring the World of Andre HHakkak’sWife: An In-Depth Look